Давайте перечислим все методы, присутствующие в Python, чтобы найти сумму квадратов NumPy. Рассмотрим их один за другим, используя несколько наглядных примеров.
Содержание
- Метод 1: с использованием вложенных циклов for
- Случай 1: с использованием вложенных циклов for
- Случай 2: сумма квадратов для двумерного массива
- Случай 3: для трехмерного массива
- Метод 2: с использованием Square() и sum()
- Случай 1: для одномерного массива
- Случай 2: для 2D-массива
- Случай 3: для трехмерного массива
- Метод 3: с использованием power() с функцией sum()
- Случай 1: 1D-массив в сумме квадратов
- Случай 2: 2D-массив в сумме квадратов
- Случай 3: 3D-массив
- Метод 4: с использованием point()
- Случай 1: для одномерного массива
- Случай 2: для 2D-массива
- Случай 3: для 3D-массива
- Метод 5: с помощью функции einsum()
- Случай 1: для одномерного массива
- Случай 2: для двумерного массива
- Случай 3: для трехмерного массива
- Метод 6: с использованием функции linalg()
- Случай 1: для одномерного массива
- Случай 2: NumPy суммирует квадрат чисел двумерного массива
- Случай 3: в 3D-массиве
Метод 1: с использованием вложенных циклов for
- Этот метод использует вложенные циклы for для перебора элементов массива NumPy в Python.
- Он вычисляет квадрат каждого элемента и добавляет его в переменную.
- Этот процесс продолжается до тех пор, пока не будут обработаны все элементы массива NumPy в Python.
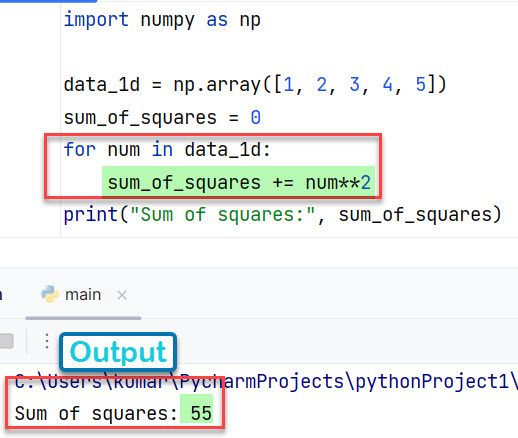
Случай 1: с использованием вложенных циклов for
Цикл for инициируется для перебора каждого числа, хранящегося в одномерном массиве. И каждое число из массива возводится в квадрат (num**2). Затем квадрат числа добавляется с помощью оператора +=.
import numpy as np
data_1d = np.array([1, 2, 3, 4, 5])
sum_of_squares = 0
for num in data_1d:
sum_of_squares += num**2
print("Sum of squares:", sum_of_squares)
Выход:
Sum of squares: 55
Скриншот вывода:
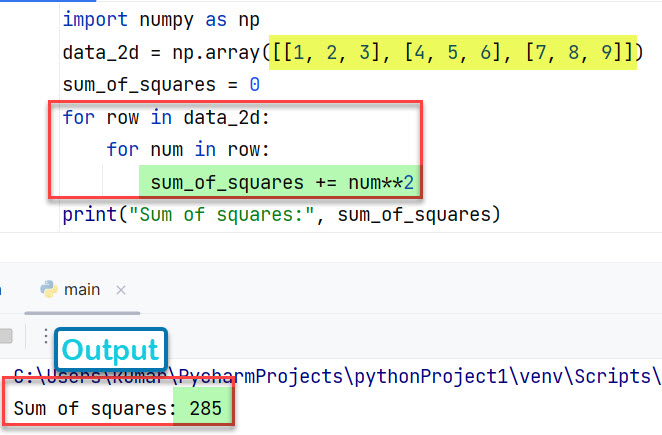
Случай 2: сумма квадратов для двумерного массива
import numpy as np
data_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
sum_of_squares = 0
for row in data_2d:
for num in row:
sum_of_squares += num**2
print("Sum of squares:", sum_of_squares)
Вывод: реализация приведенного выше кода приведена ниже.
Sum of squares: 285
Случай 3: для трехмерного массива
import numpy as np
data_3d = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
[[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
sum_of_squares = 0
for matrix in data_3d:
for row in matrix:
for num in row:
sum_of_squares += num**2
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 6930
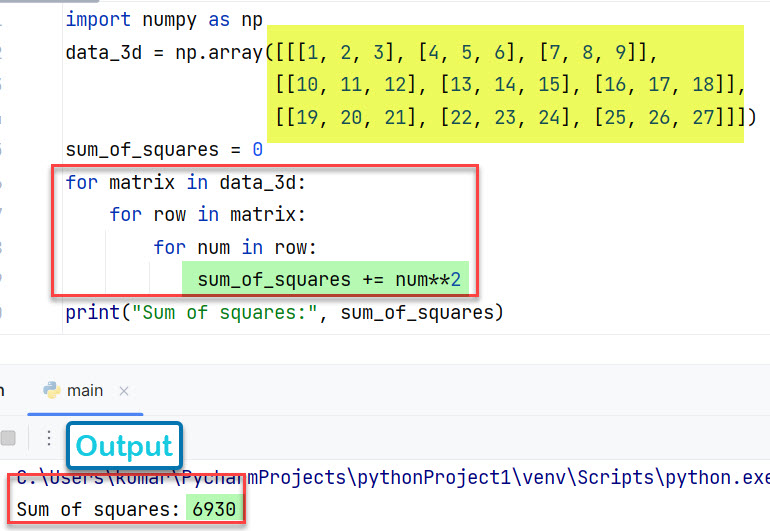
Таким образом, мы можем использовать вложенные циклы for с оператором ** и оператором += для суммы квадратов NumPy в Python.
Метод 2: с использованием Square() и sum()
- В этом методе мы сначала используем np.square() для возведения в квадрат всех элементов массива NumPy, создавая новый массив с возведенными в квадрат значениями в Python.
- Затем мы используем np.sum() для вычисления суммы всех квадратов значений в новом массиве в библиотеке Python NumPy.
- Результат сохраняется в переменной.
Случай 1: для одномерного массива
import numpy as np
data_1d = np.array([1, 2, 3, 4, 5])
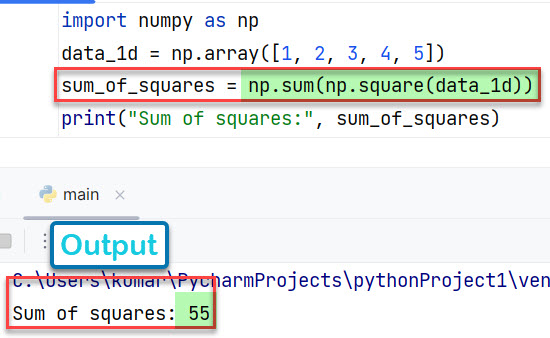
sum_of_squares = np.sum(np.square(data_1d))
print("Sum of squares:", sum_of_squares)
Результат: реализация кода суммы квадратов NumPy на Python для одномерного массива.
Sum of squares: 55
Случай 2: для 2D-массива
import numpy as np
data_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
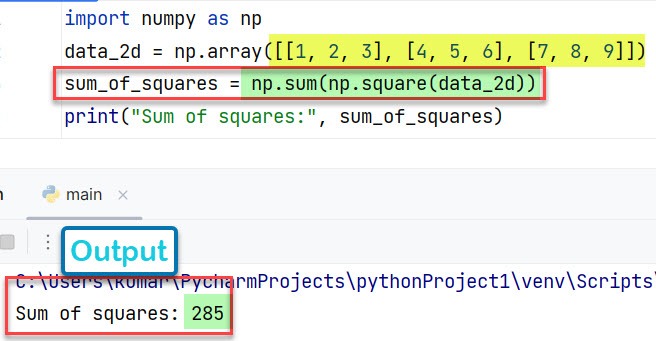
sum_of_squares = np.sum(np.square(data_2d))
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 285
Случай 3: для трехмерного массива
import numpy as np
data_3d = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
[[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
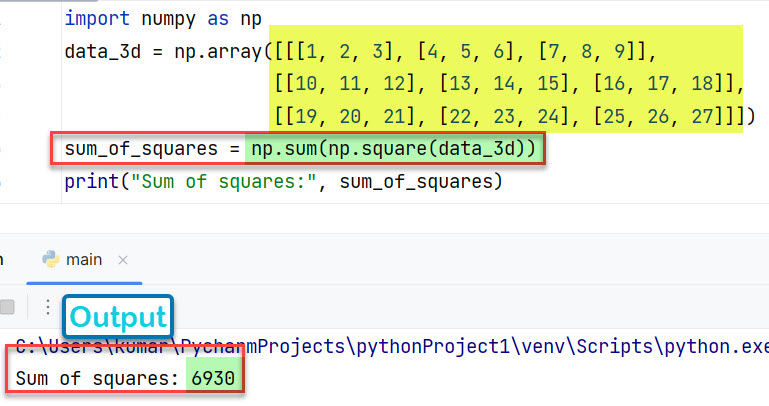
sum_of_squares = np.sum(np.square(data_3d))
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 6930
Метод 3: с использованием power() с функцией sum()
- Здесь мы будем использовать функцию numpy.power() для возведения каждого элемента массива в Python в степень 2, эффективно возводя каждое число в квадрат.
- Эта операция преобразует исходный массив в новый массив NumPy в Python, где каждый элемент представляет собой квадрат своего исходного значения.
- Затем мы берем этот новый массив квадратов значений NumPy и вычисляем его сумму с помощью функции numpy.sum(), которая складывает все значения в массиве, получая общую сумму квадратов исходного массива в Python.
Случай 1: 1D-массив в сумме квадратов
import numpy as np
array = np.array([1, 2, 3, 4])
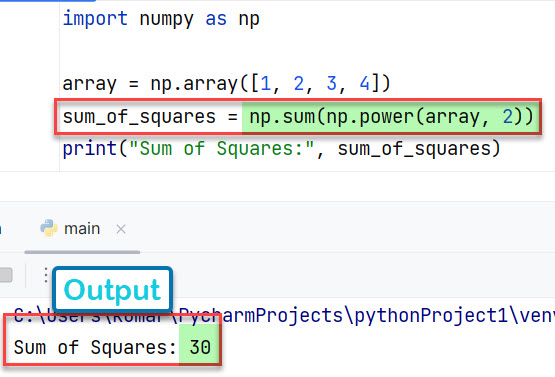
sum_of_squares = np.sum(np.power(array, 2))
print("Sum of Squares:", sum_of_squares)
Вывод:
Sum of Squares: 30
Случай 2: 2D-массив в сумме квадратов
import numpy as np
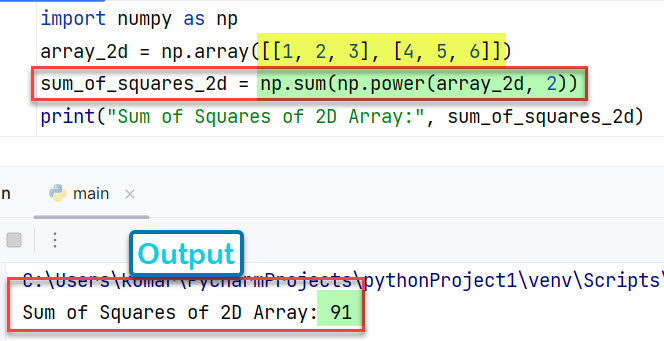
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
sum_of_squares_2d = np.sum(np.power(array_2d, 2))
print("Sum of Squares of 2D Array:", sum_of_squares_2d)
Вывод:
Sum of Squares of 2D Array: 91
Случай 3: 3D-массив
import numpy as np
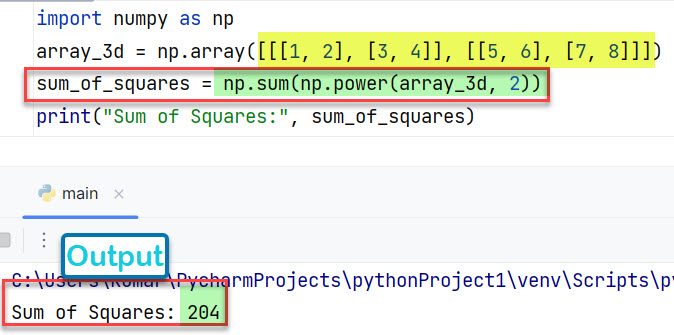
array_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
sum_of_squares = np.sum(np.power(array_3d, 2))
print("Sum of Squares:", sum_of_squares)
Вывод:
Sum of Squares: 204
Метод 4: с использованием point()
- Здесь мы выравниваем массив в NumPy Python, используя array.flatten() для создания массива в Python.
- Затем мы используем np.dot() для вычисления скалярного произведения сглаженного массива в Python на самого себя.
- Скалярное произведение по существу вычисляет сумму квадратов элементов сглаженного массива в Python.
Случай 1: для одномерного массива
import numpy as np
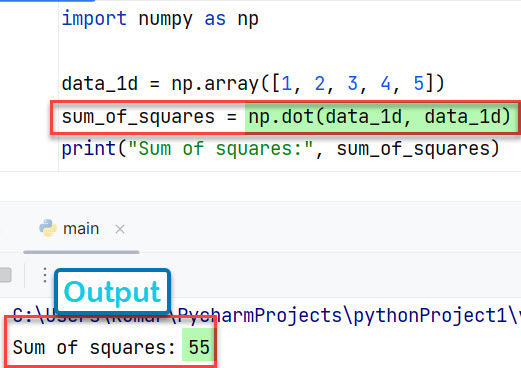
data_1d = np.array([1, 2, 3, 4, 5])
sum_of_squares = np.dot(data_1d, data_1d)
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 55
Случай 2: для 2D-массива
import numpy as np
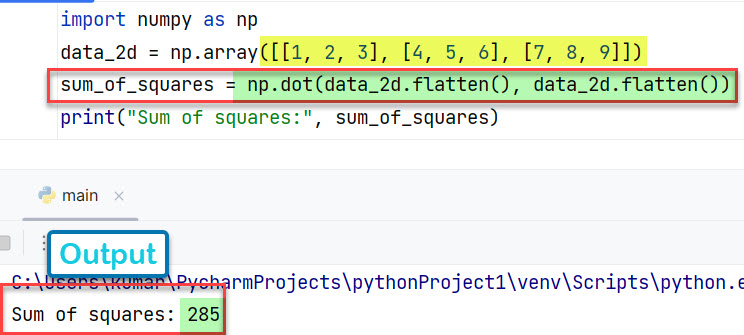
data_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
sum_of_squares = np.dot(data_2d.flatten(), data_2d.flatten())
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 285
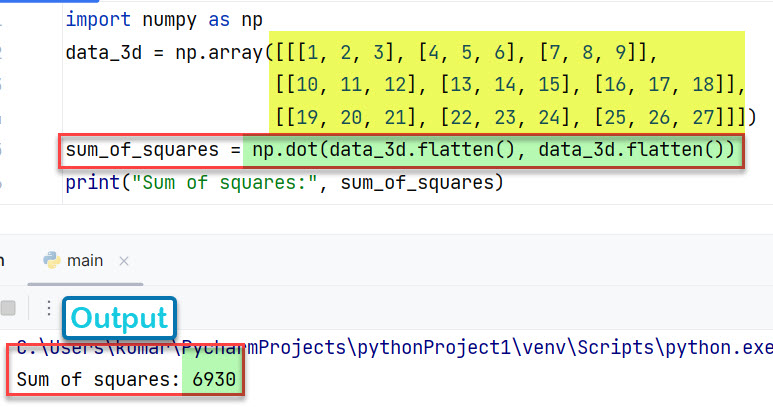
Случай 3: для 3D-массива
import numpy as np
data_3d = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
[[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
sum_of_squares = np.dot(data_3d.flatten(), data_3d.flatten())
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 6930
Метод 5: с помощью функции einsum()
- np.einsum() — мощная функция, которая может выполнять различные операции с массивами в Python.
- В этом методе мы используем np.einsum() с обозначением «ijk,ijk» для вычисления суммы квадратов в NumPy Python.
- Обозначение «ijk» указывает, что мы умножаем соответствующие элементы в массиве NumPy, а затем суммируем их с помощью Python.
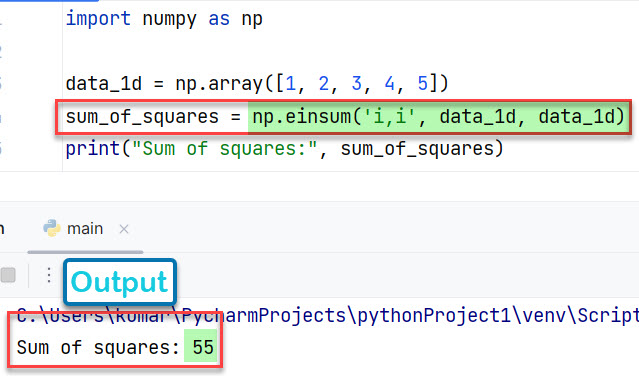
Случай 1: для одномерного массива
import numpy as np
data_1d = np.array([1, 2, 3, 4, 5])
sum_of_squares = np.einsum('i,i', data_1d, data_1d)
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 55
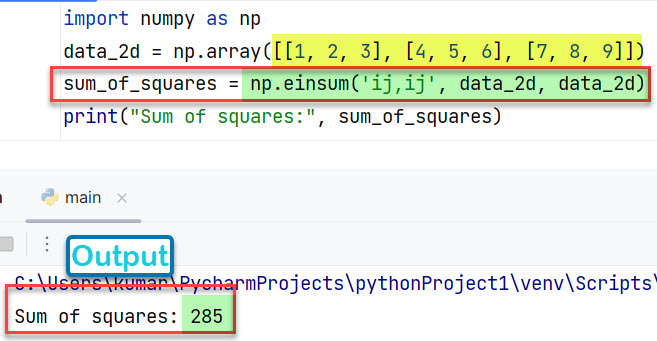
Случай 2: для двумерного массива
import numpy as np
data_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
sum_of_squares = np.einsum('ij,ij', data_2d, data_2d)
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 285
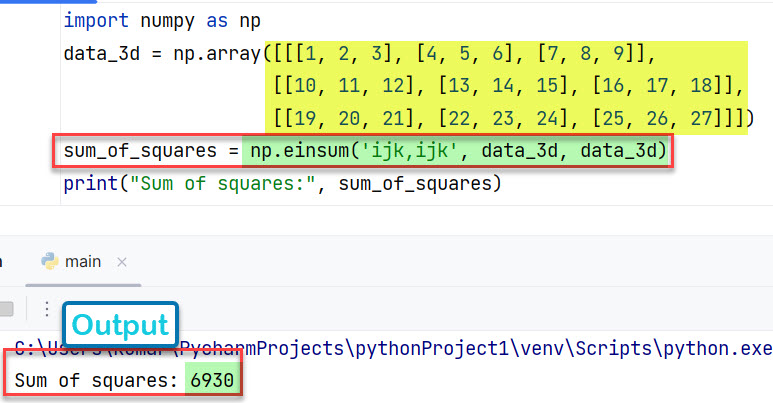
Случай 3: для трехмерного массива
import numpy as np
data_3d = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
[[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
sum_of_squares = np.einsum('ijk,ijk', data_3d, data_3d)
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 6930
Метод 6: с использованием функции linalg()
- Сначала мы выравниваем массив NumPy, используя array.flatten(), чтобы создать массив в Python.
- Затем мы используем np.linalg.norm() в библиотеке NumPy для расчета нормы L2(евклидовой нормы) сглаженного массива в Python.
- Возведение в квадрат нормы L2 дает нам сумму квадратов элементов сплющенного массива.
Случай 1: для одномерного массива
import numpy as np
data_1d = np.array([1, 2, 3, 4, 5])
sum_of_squares = np.linalg.norm(data_1d)**2
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 55.0
Случай 2: NumPy суммирует квадрат чисел двумерного массива
import numpy as np
data_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
sum_of_squares = np.linalg.norm(data_2d.flatten())**2
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 285.00000000000006
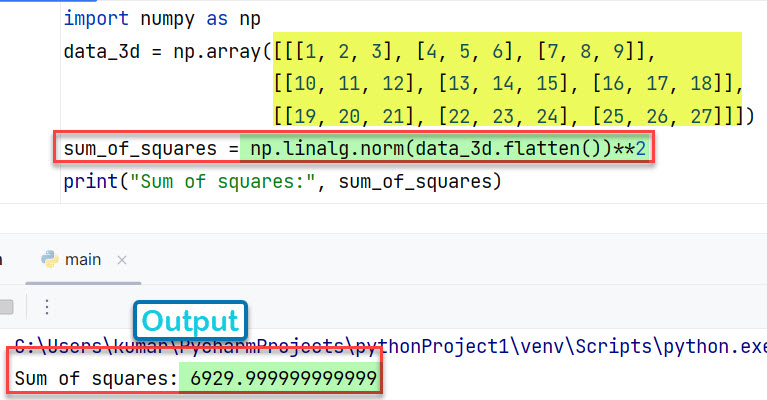
Случай 3: в 3D-массиве
import numpy as np
data_3d = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
[[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
sum_of_squares = np.linalg.norm(data_3d.flatten())**2
print("Sum of squares:", sum_of_squares)
Вывод:
Sum of squares: 6929.999999999999